Application Algorithm

You've now seen an example of our application with Bob and Carol becoming the leaders. This section will dig into the details of how the application works.

In order to create the ownership chain we're going to use a combination of hashes and digital signatures. We'll do a quick overview of both of those cryptographic primitives.

Cryptographic Hash Functions

Hash functions are functions that map data of arbitrary size to a fixed size. A cryptographic hash function is a hash function that is a one-way function who result is indistinguishable from random. A one-way function is a function where it is easy to compute in one direction but it is extremely difficult to compute the inverse function. For example, given a function f(x) => y, y is easy to generate given the function f and input x. However it is extremely difficult (and for good CHFs intractable) to calculate x given only y and f.

In terminology, the input to a hash function is known as a preimage. When the preimage is run through the hash function it produces a digest.

Bitcoin and Lightning Network frequently use the SHA-256 hash function. This function results in a 32-byte (256-bit) output. For example, if we use the SHA-256 hash algorithm we can see the 32-byte hex encoded digest.

sha256("a") = ca978112ca1bbdcafac231b39a23dc4da786eff8147c4e72b9807785afee48bb
sha256("b") = 3e23e8160039594a33894f6564e1b1348bbd7a0088d42c4acb73eeaed59c009d

As we discussed, there is no way to to derive the preimage a given the digest ca978112ca1bbdcafac231b39a23dc4da786eff8147c4e72b9807785afee48bb or to derive the preimage b given the digest 3e23e8160039594a33894f6564e1b1348bbd7a0088d42c4acb73eeaed59c009d.

If we combine the preimages to make ab we get a new digest that is in no way related to the digests of the individual preimage components.

sha256("ab") = fb8e20fc2e4c3f248c60c39bd652f3c1347298bb977b8b4d5903b85055620603

Cryptographic hash functions enable us to do interesting things like hide information in the digest that can be verified with knowledge of the preimage. We see this in action with invoices and HTLC payments. We'll leverage this information hiding/revealing to selectively build the preimage for our hash.

Elliptic Curve Digital Signature Algorithm (ECDSA)

This application will also make use of digital signatures created using the elliptic curve digital signature algorithm over the curve secp256k1. This is the curve that Bitcoin and Lightning Network use for digital signatures. We're not going to get into the specifics of how digital signatures work but if you want to deep dive, I recommend reading Chapters 1-3 of Programming Bitcoin by Jimmy Song.

The quick hits are that a private key can be used to generate a public key. This public key can be public knowledge. Only the holder of the private key is capable of generating the public key.

A signature is created for some piece of data, we'll refer to it as z using the private key. The signature can be shared publicly.

When a signature is combined with a public key it can be used to verify that the signature was indeed created by owner of that public key.

Given just the signature (and a bit of extra metadata), it is also possible to derive the public key that was used to create the signature. When a Lightning Network node verifies a signature it will derive the public key from the signature and verify it against the network graph database that contains all of the public keys for the network. We'll be using signature creation and validation in our application.

Our Algorithm

In our application we'll be using both digital signature and hashes to construct a chain of ownership. The basis of this chain is that the preimage from the last-settled invoice is used as an identifier of the next link. In a sense this creates a hash-chain of ownership.

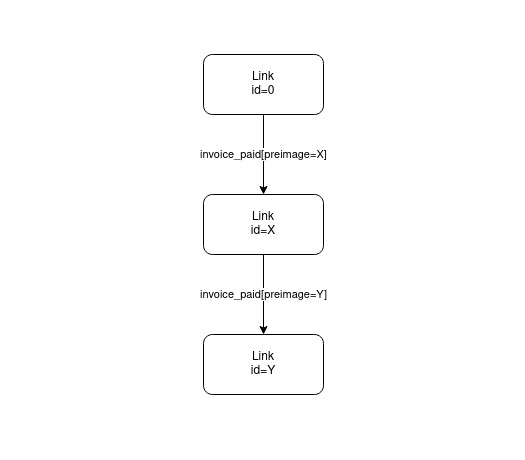
This diagram shows you that the first link starts with some arbitrary id, in this case id=0. We start with an arbitrary identifier because there was no prior state. In each link, many invoices can be generated using this identifier. Each invoice will have a unique preimage that ties it to the user that wants to pay the invoice. When an invoice is finally paid (say with preimage=X for instance) a new link is generated and the identifier of the new link becomes the preimage of the settled invoice (so id=X for this example). So as you can see, when an invoice is paid, its preimage becomes identifier of our application.

Unlike in simple invoice payments (that we saw earlier), the preimage is not going to be arbitrarily generated by our Lightning Network node. We need to tie each invoices to a specific users for the current state of the game. We need to ensure that:

1. Each invoice in a link has a unique preimage and hash, eg if Alice and Bob both want to become the leader they should get different invoices.
2. It is not possible to guess the preimage for an invoice
3. A leader can reconstruct the preimage using information that only they can generate once a payment has been made. This provides proof of ownership beyond possession of the preimage.

So let's explore the actual construction.

Alice is running the server for our application. She initiates the service with some seed value. Alice signs a message with the seed and keeps her signature to herself for now. Alice can always easily regenerate this signature if she needs to by resigning the seed.

Bob accesses Alice's website, and discovers that he can become the leader by

1. Creating a signature using his Lightning Network node where the message is the seed
2. Sending this signature to Alice's application

Alice's application verifies Bob's signature, making sure it is a valid signature for the seed and she sees that it's from Bob. As we talked about, only Bob will be able to generate this signature, but anyone can verify that the signature is valid and from Bob.

Alice now creates an invoice preimage by concatenating her signature for the seed, Bob's signature for the seed, and the satoshis that Bob is willing to pay.

preimage = alice_sig(seed) || bob_sig(seed) || satoshis

The only issue is that the Lightning Network invoices require the preimage to be 32-bytes. We get around this by simply using hashing to contain the value within 32-bytes:

preimage = sha256(alice_sig(seed) || bob_sig(seed) || satoshis)

Then our hash digest in the invoice is the hash of the preimage:

hash = sha256(preimage)
hash = sha256(sha256(alice_sig(seed) || bob_sig(seed) || satoshis))

Alice sends Bob the invoice. Bob wants to take ownership, so he pays the invoice and receives the preimage as proof of payment.

At this point, Bob can prove that he paid the invoice since he has the preimage, but he can't reconstruct the preimage. Alice needs to publish her signature to the website for Bob to be able reconstruct the preimage. Ideally we would have a scheme where Bob can prove ownership without needing out-of-band information, something encoded directly in the preimage itself. A fun thought experiment for later.

So how does Carol take over ownership? In order to do this, Alice application now advertises Bob's preimage as the current state. Carol can sign Bob's preimage and perform the same upload/pay invoice that Bob did. Once she completes the payment, the preimage for Carol's paid invoice becomes the new leading state of the game.

Now that may be a lot to unpack, so you may want to go through it a few time. And don't worry, after a few goes at making Bob and Carol the leaders it will hopefully become more intuitive.